
Moments of Inertia for a rectangular plane with axis through center can be expressed as R = radius in sphere (m, ft) Rectangular Plane R = distance between axis and hollow (m, ft) Solid sphere R = distance between axis and outside disk (m, ft) Sphere Thin-walled hollow sphere R = distance between axis and outside cylinder (m, ft) Circular Disk R o = distance between axis and outside hollow (m, ft) Solid cylinder R i = distance between axis and inside hollow (m, ft) R o = distance between axis and outside hollow (m, ft) Hollow cylinder R = distance between axis and the thin walled hollow (m, ft) Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass (1) and can be expressed as: Some Typical Bodies and their Moments of Inertia Cylinder Thin-walled hollow cylinder Radius of Gyration in Structural Engineering I = moment of inertia for the body ( kg m 2, slug ft 2) The Radius of Gyration for a body can be expressed as The Radius of Gyration is the distance from the rotation axis where a concentrated point mass equals the Moment of Inertia of the actual body. K = inertial constant - depending on the shape of the body Radius of Gyration (in Mechanics) + m n r n 2 (2)įor rigid bodies with continuous distribution of adjacent particles the formula is better expressed as an integralĭm = mass of an infinitesimally small part of the body Convert between Units for the Moment of InertiaĪ generic expression of the inertia equation is I = ∑ i m i r i 2 = m 1 r 1 2 + m 2 r 2 2 +. Point mass is the basis for all other moments of inertia since any object can be "built up" from a collection of point masses. = 1 kg m 2 Moment of Inertia - Distributed Masses The Moment of Inertia with respect to rotation around the z-axis of a single mass of 1 kg distributed as a thin ring as indicated in the figure above, can be calculated as
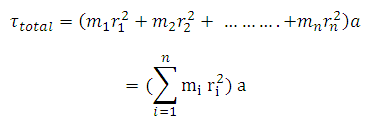
MOMENT OF INERTIA EQUATION FREE
Make 3D models with the free Engineering ToolBox Sketchup Extension R = distance between axis and rotation mass (m, ft) Example - Moment of Inertia of a Single Mass I = moment of inertia ( kg m 2, slug ft 2, lb f fts 2)



 0 kommentar(er)
0 kommentar(er)
